Stel, je wandelt over een netwerk van paden die louter uit zevensprongen bestaan. Op elke kruising die je tegenkomt komen zeven paden samen (inclusief het pad waar je net vandaan kwam), netjes in gelijke hoeken verdeeld:

Aan het eind van elk pad van een zevensprong onspringt weer een nieuwe zevensprong; aan die zevensprongen zitten weer nieuwe zevensprongen vast, etc. Hoe ziet het patroon eruit (ik noem het maar even een heptaweb) dat je dan krijgt?
Laten we het eens bouwen. Dus, aan het eind van elk pad van een zevensprong plaatsen we een nieuwe zevensprong, zodanig dat de paden recht aansluiten:
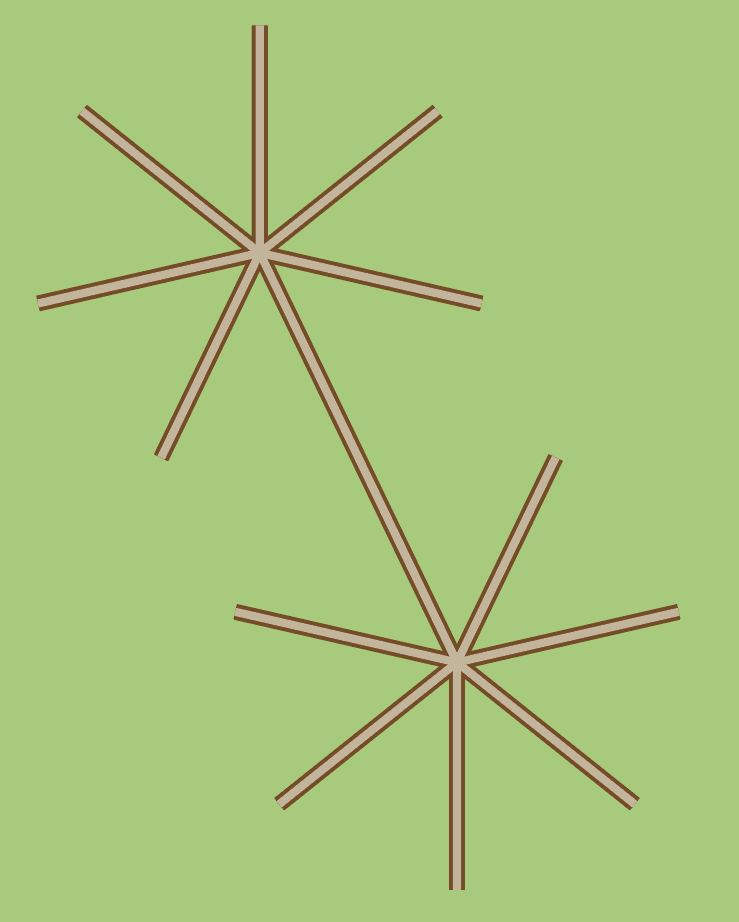
En zo het hele rondje rond:
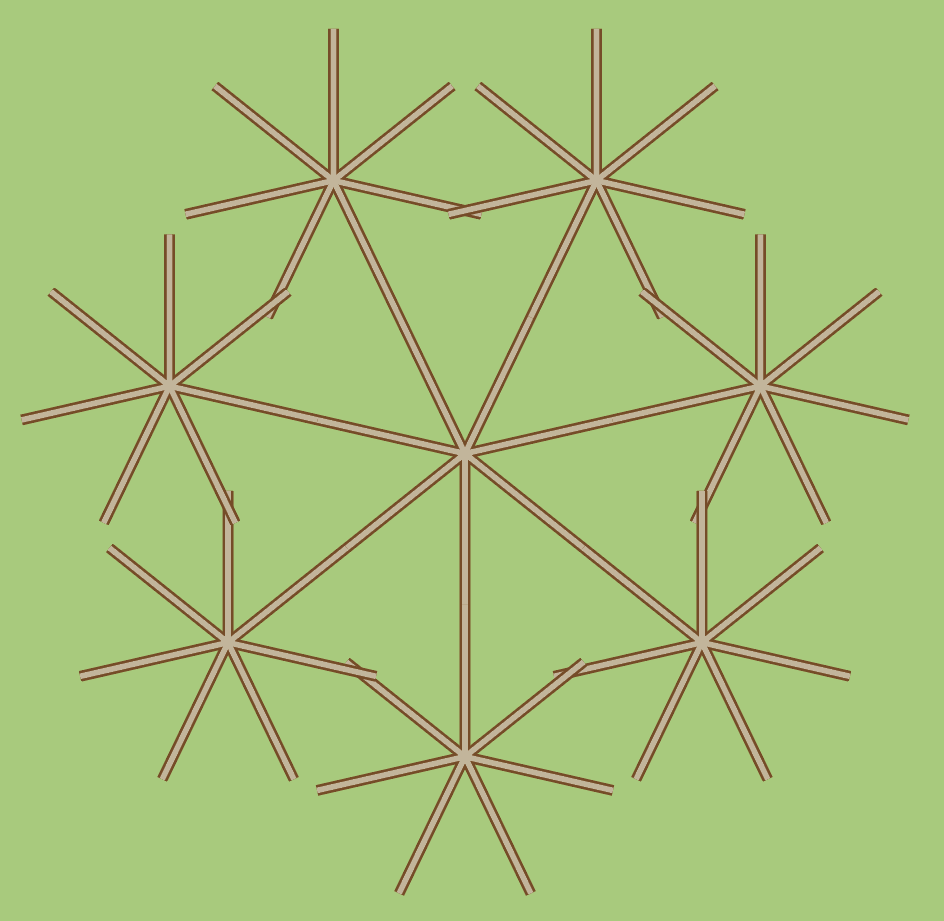
U ziet, we krijgen nu kruisende paden, maar we stellen ons voor dat die over elkaar heen lopen (middels bruggetjes, tunnels, alternatieve dimensies, ziemaar) en geen gelijkvloerse splitsingen opleveren waar de wandelaar onverhoopt zou kunnen afslaan.
De volgende generatie doen we weer precies zo: aan het eind van elk van de tweeënveertig uiteinden (want 7 × 7, min 7 voor de zevensprong in het midden die we al hadden) plaatsen we weer nieuwe zevensprongen:

En met nog een generatie erbij (en de lijntjes dun voor beter overzicht) krijg je dit:

Juist. Dat wordt dus binnen de kortste keren ridicuul complex, en daarmee machtig interessant. Hoe ver kun je hiermee doorgaan? Komt het patroon vroeg of laat weer op zichzelf uit (bijvoorbeeld na zeven of veertien generaties), of loopt de complexiteit oneindig op en vult uiteindelijk het hele vlak zich met lijnen? Ik weet het niet, er zal ongetwijfeld onderzoek naar zijn gedaan, niet in de laatste plaats door islamitische patronenbedenkers.
Ik heb deze plaatjes handmatig in elkaar zitten pielemieren; programmeren in iets als Processing is natuurlijk stukken netter en efficiënter en dan weet je in een muisomdraai hoe diep het konijnenhol gaat, maar dan moet ik eerst even leren hoe dat moet. Daarover misschien eens later.
Maar waarom dan, Drab?
Nou, omdat patroontjes altijd reden tot feest zijn natuurlijk. Nee, maar, ik was aan het knutselen aan een schriftsysteem met vormen die zich op zo’n zevenvoudig rooster bevinden, zodoende. Ik denk, ik doe eens wat spannenders dan driehoeken, vierkanten of zeshoeken:
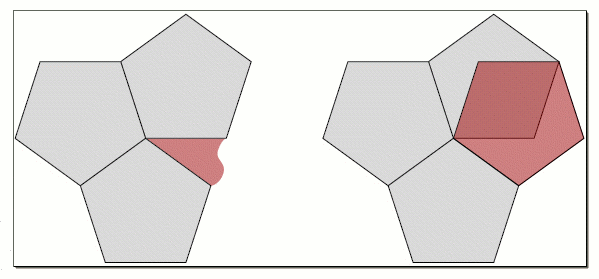
Zoals bekend zijn dat de enige regelmatige veelvlakken waarmee je naadloos een muur/vloer kunt betegelen. Neem enig ander regelmatig veelvlak – vijfhoeken, zevenhoeken of alles daarboven – en je raakt in de problemen: er ontstaan gaten tussen je tegels, die niet met diezelfde tegels te dichten zijn zonder ze met elkaar te laten overlappen:
Een vijf-, zeven- of hogervoudig rooster geeft dus onherroepelijk complexe situaties en daar houden wij van (zolang het niet het echte leven betreft natuurlijk). Zo moet het complete heptaweb per definitie ook dit soort kringetjes in zich huisvesten:
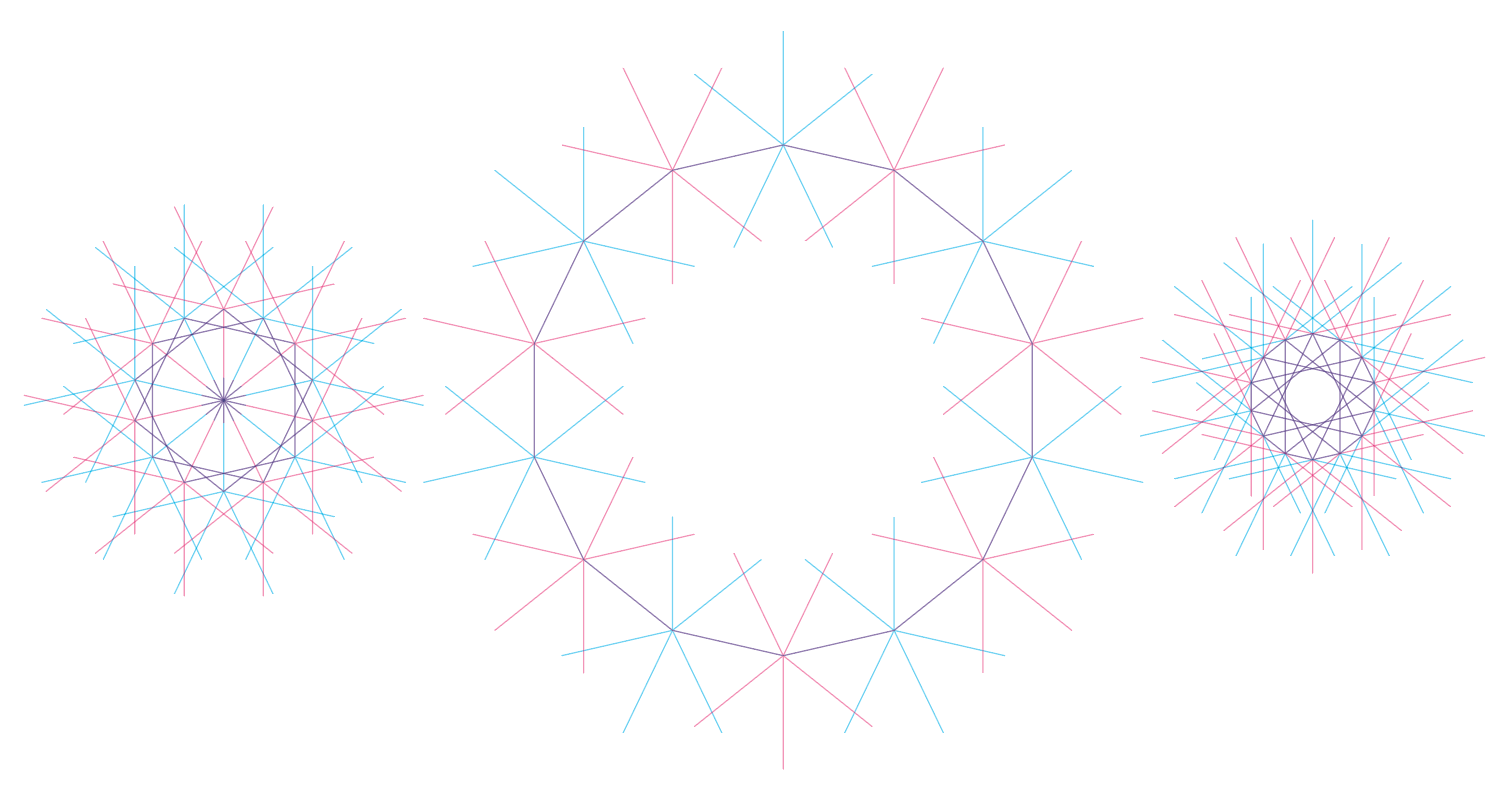

Dus, mocht het schrift niks worden (het heet Heptawirwar, omdat het principe hetzelfde is als bij Wirwar, maar dan hepta) houden we er in ieder geval een leuk zijspoor met intrigerende plaatjes aan over. Kijk, met opgepimpte kleuren wordt het ook wel lekker kosmisch:



Ha, ik zit al sinds december in een origamisterrenfase, begon met vouwen van zeshoekige blaadjes, ontdekte dat als je je blaadjes zelf inkleurt elke ster een kaleidoskopisch kinderei wordt, en toen natuurlijk ook uitproberen wat er gebeurt als je dezelfde ster van een heptagon (of driehoek, of pentagon, of octagon) vouwt. Veelhoeksinteractie is het nieuwe bij de fontijn hangen!
LikeGeliked door 1 persoon
Ha, ja, dit soort dingen zijn ook zwaar origamiverantwoord ja! Al zou ik Tadashi Tokieda even moeten bellen om te vragen hoe je dingen met zevenvoudige symmetrie kan vouwen.
LikeLike