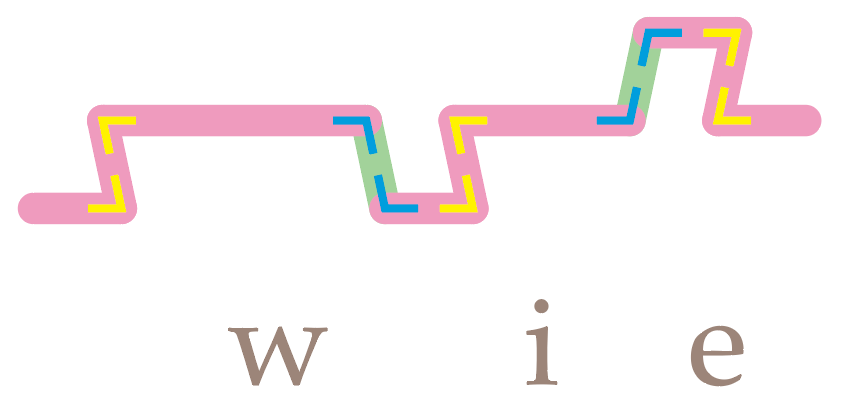Triptrap

Triptrap is een schrifsysteem waarbij de letters trapjes vormen, die worden samengevoegd tot langere trapjes. Bijvoorbeeld:

Stijgende en dalende treden

Ja maar wacht eens even Drabkikker, hoe kan het dat die twee p’s niet hetzelfde vormpje hebben, en die e’s en n‘en en die ene i ook niet, en hoe kunnen de g en de e erna juist weer precies hetzelfde teken lijken te zijn?

Goed gezien, lezer! Dat komt namelijk omdat de letters geen vastgelegde vorm hebben, maar worden gedefinieerd in termen van stijgen en dalen van de traptreetjes ten opzichte van hun buurtreetjes. Triptrap is een voorbeeld van wat ik een relatief schriftsysteem noem (ik heb er meer, zoals Wirwar en XOR en Relatieve kleurcode): letters hebben een vaste onderliggende beschrijving, maar hoe die zich precies tot concrete vormen manifesteert hangt af van de context.

Bij Triptrap werkt het zo:

• De lettertrapjes bevinden zich op regels die bestaan uit een denkbeeldig drietal lijnen: een bovenlijn, een middellijn en een onderlijn. Trapjes mogen niet boven of onder deze lijnen uitsteken:

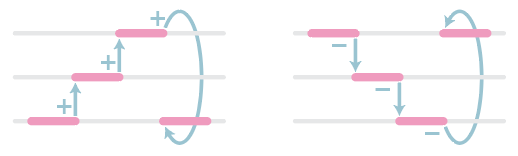
• Elke letter kan worden omschreven met een code als +2-1. De plus betekent “ga één lijn omhoog” ten opzichte van de vorige trede, de min staat voor “ga één lijn omlaag”; de cijfers geven de breedtes van de treden aan (variërend van 1 t/m 3). +2-1 staat dus voor een lettertrapje waarbij de eerste trede hoger ligt dan zijn voorganger en breedte 2 heeft, en de tweede trede lager ligt dan de eerste en breedte 1 heeft. (Dit trapje staat voor de letter d, voor wie er benieuwd naar was. Zie verderop voor het hele alfabet.)

• Op welke hoogte de treden van een letter komen te liggen hangt dus af van de hoogte waarop de voorgaande trede zich bevindt. Als de voorgaande trede (hieronder weergegeven met het smalle lijntje links) bijvoorbeeld op de onderlijn ligt, dan ziet een d (code +2-1) er zo uit:

• Ligt de voorgaande trede daarentegen op de middellijn, dan krijgt de d dezelfde vorm als daarnet, maar komt hij in zijn geheel één lijn hoger te liggen:

• Maar dan. Wat te doen als de voorgaande trede op de bovenlijn ligt? De eerste trede van de d zou dan nóg een lijn hoger moeten komen te liggen, maar dat kan niet: Triptrapvormen mogen immers niet boven of onder hun drielijnige regels uitsteken.
  
  Daarom geldt in zulke gevallen: ten opzichte van de bovenlijn betekent het plusje “ga naar de onderlijn” en ten opzichte van de onderlijn betekent het minnetje “ga naar de bovenlijn”. Alsof de + en – zich zegmaar via de derde dimensie om de regel heen wikkelen:

• Zodoende dat een d ten opzichte van een trede op de bovenlijn er heel anders uitziet dan zijn andere twee verschijningsvormen hierboven: de eerste trede gaat ‘omhoog’ en landt op de onderlijn; de tweede trede gaat vervolgens weer ‘omlaag’ en komt uit op de bovenlijn:

Zo snappen we waarom de letters in bijvoorbeeld pijpleidingen niet overal dezelfde vorm hebben. De i bijvoorbeeld heeft weliswaar telkens de code -1+2, maar bij de eerste i wordt die gerekend vanaf de bovenlijn (want daar eindigt de p links ervan); bij de de tweede i moeten we rekenen vanaf de onderlijn (vanwege zijn linkerbuurman e) en idem evenzo voor de derde i (aangezien de d daar eindigt):

Ook wordt nu duidelijk waarom de g en de e er identiek uitzien: de g is een -1-1 ten opzichte van de onderlijn, dus zijn eerste trede belandt (via het ‘derde dimensie’-wormgat) op de bovenlijn en zijn tweede trede op de lijn daaronder; de e is een +1-1 ten opzichte van de middellijn (want daar eindigt de g), wat hier toevallig precies hetzelfde vormpje oplevert als voor de g.

Het alfabet (code)

En zo gaat het met alle letters. Een letter heeft altijd dezelfde onderliggende code, maar hoe die exact vorm krijgt wordt bepaald door de letter die eraan voorafgaat. De codes voor het hele alfabet (plus cijfers) zijn als volgt:

a	+1-2	m	+2+1	y	-3-1
b	-3+1	n	-1+1	z	+1-3
c	+1+3	o	+2-2	1	+3-2
d	+2-1	p	-1-3	2	-3+2
e	+1-1	q	-2+3	3	-2-3
f	+3+1	r	-2+2	4	+2+3
g	-1-1	s	+1+2	5	+3+2
h	-1-2	t	-2+1	6	-3-2
i	-1+2	u	+3-1	7	+3-3
j	-2-2	v	-2-1	8	-3+3
k	+2+2	w	-1+3	9	-3-3
l	+1+1	x	+2-3	0	+3+3

Het alfabet (visueel)

In plaats van dit hele codeverhaal kunt u ook droogweg onthouden dat elke letter drie mogelijke verschijningsvormen heeft, afhankelijk van de hoogte van de voorgaande trede:

Twee van de mogelijke vormen die een letter kan krijgen lijken erg op elkaar en verschillen alleen in de hoogte waarop ze staan, plus een derde vormpje dat er heel anders uitziet omdat het een ‘dimensie’-sprong maakt van boven- naar onderlijn of vice versa. Maar de breedtes van de twee treden zijn voor alle drie de vormvarianten van een letter altijd dezelfde.

Mededelingen schrijven

Om een woord te schrijven neem je de afzonderlijke letters in hun correcte relatieve verschijningsvorm, en verbindt ze vervolgens met verticale lijnen. Als vaste regel geldt: de eerste letter van een boodschap krijgt altijd de vorm gerekend vanaf de middellijn (vandaar dat die vorm in het alfabet hierboven steeds als eerste staat gegeven):

Eventuele verdere woorden die volgen blijven onverbonden met hun buurwoorden: het ontbreken van het verticale verbindingsstuk fungeert als spatie. De woorden mogen hierbij dichter naar elkaar toe worden geschoven, als daar ruimte voor is.

Maar, opgelet: de eerste letter van elk nieuw woord krijgt de vorm gerekend ten opzichte van de laatste trede van het vorige woord. Je begint dus niet per definitie per woord steeds opnieuw te rekenen vanaf de middellijn, maar vanaf de lijn waarop de tweede trede van de laatste letter van het vorige woord zich maar moge bevinden (wat natuurlijk ook de middellijn kan zijn). Zodoende dat bijvoorbeeld de twee is‘jes in Wie niet weg is is gezien er totaal verschillend uitzien:

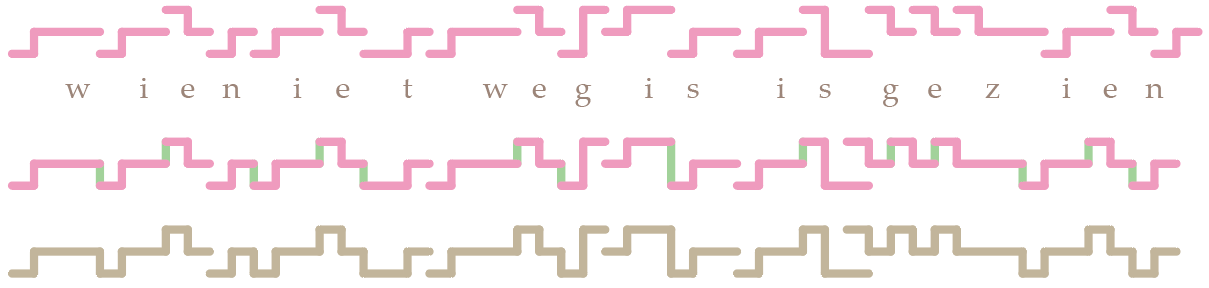
Hellende lijnen voor betere ontcijferbaarheid

Goed, maar Drabkikker, hoe zie je in zo’n letterkronkel nou in vredesnaam nog waar de ene letter eindigt en de volgende begint? Als verticale lijnen zowel delen van een letter kunnen zijn als verbindingsstukken ertussen, dan raak je toch binnen de kortste keren de draad kwijt? Wat een flutschrift, Drabkikker, we zijn beter van je gewend.

Ik ook, bezoeker! Dat is inderdaad een storende zwakte, en daarom gebruik ik de volgende truc om die het hoofd te bieden: ik laat de verticale lijnen een beetje hellen, zodanig dat lijnen die binnen letters vallen onderling scherpe hoeken maken, en verbindingsstukken tussen letters stompe hoeken:

Het kan natuurlijk ook andersom (stompe hoeken binnen letters, scherpe ertussen); op zich allebei prima en ik ben er nog niet helemaal uit wat logischer voelt:

Van dit lijnengehel worden de trapjes leuk trippy, wat meteen de naam van het schrift nader bestaansrecht verleent. Het heeft ook wel iets van varende bootjes her en der.