Ik ben bij lange na geen rekenwonder. Bij getallen boven de 4892 haak ik al vrij rap af en ik ben minstens een minuut aan het hoofdratelen op simpele sommetjes als 114 – 97. Toch smeult er een vuurtje in mij dat hevig kan oplaaien waar het de onderliggende concepten van de wiskunde betreft.
Zo ben ik een tijdje geleden weer eens hergeïnteresseerd geraakt in priemgetallen. Priemgetallen zijn echt hele rare dingen. Vooral omdat ze er zo normaal uitzien. Totdat je ze probeert open te snijden en ze net zo op gewone getallen blijken te lijken als de kleuren van de regenboog op wit licht.
Ondeelbaar
Het begint allemaal met erwtjes. (Erwwwtjes, wat is dat voor bespottelijk woord? Flippo’s mag ook. Of jujubes.) Neem twaalf mariakaakjes. Leg ze in een rechthoek. Twee bij zes, drie bij vier, mag allemaal.

Probeer hetzelfde bij 13. Dat gaat dus niet. Dertien contactlenzen zijn op geen enkele manier in een rechthoek te leggen: je komt steeds tekort of je hebt te veel:
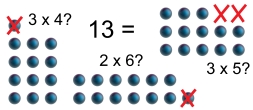
Het enige wat je met 13 kunt is een lijn leggen, van 1 bij 13 of 13 bij 1:

En daar zit hem het belangrijke verschil. De wereld van natuurlijke getallen (1, 2, 3, 4, 5, etcetera) is onder te verdelen in twee supercategorieën: ‘rechthoek’-getallen zoals 12, en ‘lijn’-getallen zoals 13, beter bekend als priemgetallen. Rechthoekgetallen kun je delen door andere getallen. Priemen niet: die zijn alleen maar deelbaar door zichzelf of 1, verder door niks of je krijgt een breuk.
Ongrijpbaar
Dit ogenschijnlijke onbenulligheidje verleent priemgetallen een intrigerende ongrijpbaarheid. Precies omdat je ze niet kunt delen kun je ze ook niet voorspellen. Het is van tevoren niet te zeggen of een getal priem is of niet: de enige manier om daar achter te komen is stomweg alle lagere getallen langslopen en kijken of je je kandidaat erdoor kunt delen.

Voor een getal als 21 is dat nog wel te doen. Deelbaar door 2? Nee. Deelbaar door 3? Ja. Niet priem dus. Bij 101 is het al beduidend meer gedoe. Deelbaar door 2? Nee. Deelbaar door 3? Nee. […] Deelbaar door 99? Nee. Deelbaar door 100? Nee. Priem dus! Allemachtig zeg. Zelfs met de kennis dat u de even getallen mag overslaan (die zijn immers altijd deelbaar door 2) kunt u zich voorstellen dat dit boven de 2305843009213693951 een beetje tijdrovend proces wordt.
En toch is er, enkele ruwe handgrepen daargelaten (klik bijvoorbeeld op de animatie hierboven), geen simpeler methode. Computers doen het rapper dan mensen, maar zijn uiteindelijk tot dezelfde dommekrachtsmethode veroordeeld: elk nieuw getal moet apart op priemheid worden getest. Projecten als GIMPS ontdekken eens in de paar jaar een nieuwe priem, zo traag gaat het. De hoogst bekende is momenteel 243112609 – 1 (hij is wat te groot om voluit te schrijven); u kunt zelf mee helpen zoeken naar de volgende en uw 40.000 dollar vindersloon spontaan doneren aan bloggers die leuke stukjes over priemgetallen schrijven.

Uniek
Goed, je kunt ze niet delen, vermenigvuldigen kun je priemen uiteraard wel. Het resultaat is dan natuurlijk per definitie een niet-priem: de uitkomst van een vermenigvuldiging is immers deelbaar door de getallen die je zojuist met elkaar hebt vermenigvuldigd.
Op deze manier kun je nieuwe getallen bouwen. Dit lijkt flauw: met niet-priemen kun je dat immers even goed? Maar daar zit hem de gein: met priemen kun je niet zomaar een beetje getallen bouwen, maar alle andere natuurlijke getallen die er zijn.
Hoebedoelu? Wel: neem maar eens een willekeurig niet-priemgetal. 15 is goed, of 18, of 84, of 1848. Een laag getal is makkelijker, maar het werkt net zo goed bij hogere. Herschrijf nu dat getal als een vermenigvuldiging van priemen. Voor 15 wordt dat bijvoorbeeld 3 x 5, allebei priemen. 18 is evenzo te herschrijven als 2 x 2 x 3 (eenzelfde priem mag meermalen voorkomen). 84 wordt 2 x 2 x 3 x 7; 1848 is 2 x 2 x 2 x 3 x 7 x 11. De onderlinge volgorde van de priemen doet er niet toe.
Wat u hier aan het doen bent heet het ontbinden van getallen in priemfactoren (kortweg factoren). Probeer het bij welk niet-priemgetal u maar wilt: u zult merken dat het altijd herschrijfbaar is als een product van priemen. Misschien twee priemen, misschien vijfenzestig, maar het gaat altijd op. Niet-priemgetallen heten hierom ook wel samengestelde getallen: samengesteld uit priemen.
Dat je elk willekeurig getal zo in factoren kunt ontbinden is op zich al tamelijk opmerkelijk (gezien het feit dat er oneindig veel getallen zijn), maar het wordt nog curieuzer. Neem dezelfde getallen als daarnet, en probeer ze nu eens op een àndere manier in priemen te ontbinden. Toe, probeer het maar.
Dat gaat dus niet! 15 heeft als enige priemfactoren 3 en 5; 18 heeft alleen 2, 2 en 3. De enige manier om 84 te ontbinden is 2 x 2 x 3 x 7; 1848 is alleen op te hakken als 2 x 2 x 2 x 3 x 7 x 11.
Wat we hier bij de kladden hebben is niet enkel-, maar dubbelvoudig speciaal. Welk getal u ook neemt, of het nu 6 is of 288 of 999999991 of honderd miljoen miljard, het zal a) altijd te ontbinden zijn in priemen, en b) ook alleen maar in die specifieke priemen!
Dit is echt best wel apart. Er is onder alle natuurlijke getallen die bestaan (alle ∞ dus) niet één dat niet als priemen is te schrijven, en niet één dat stiekem twee oplossingen heeft. Niet eentje. Carl Friedrich Gauss heeft het bewezen: Elk natuurlijk getal kan op slechts één manier geschreven worden als een product van priemgetallen. Doe dat maar eens na, zo’n bewijs leveren terwijl we niet eens weten waar de eerstvolgende priem zal opduiken. Deze ontdekking is dermate fundamenteel dat het de Hoofdstelling van de Rekenkunde wordt genoemd.
Dit filmpje legt het nog eens uit, en beantwoordt meteen uw brandende vraag waarom 1 geen priem is:
Fundamenteel
Begint u een beetje te vatten waarom ik priemen echt hele rare dingen noemde? Hier hebben we een zootje ongrijpbare, onvoorspelbare nonconformisten van getallen—we snappen ternauwernood waarom ze er überhaupt zijn—en dat loopt doodleuk het fundament van alle natuurlijke getallen te wezen!
Er is geen enkele reden waarom dit zo zou moeten zijn, en toch is het zo. Priemen zijn ondeelbaar en tegelijk de bouwstenen waar al het andere van is gemaakt.

Dit maakt ze letterlijk tot de atomen (ἄτομος: ‘niet-deelbaar’) van de getallenwereld. Elk samengesteld getal is als een molecuul met zijn eigen unieke opbouw uit niet verder te splitsen priem-atomen. Zie bijvoorbeeld de samengestelde getallen hieronder: 14 bestaat uit de priemen twee en zeven; 45 uit drie, drie en vijf; 288 uit vijf tweeën en twee drieën. Vermenigvuldig de atomen en zie het voor uzelf.

Of je breit er een factortrui van. Kan ook.
Smaak- en kleurrijk
Op school wordt ons geleerd dat getallen iets zijn met een grootte. Zeven is groter dan zes, tweeëndertig is kleiner dan achtduizendvier, en daarmee is de kous wel zo’n beetje af. Maar dat die grootte een getal de fascinerendste karaktertrekken meegeeft wordt er doorgaans niet bij verteld. Aan de ingewanden van de getallen wordt gevoeglijk voorbijgegaan, terwijl daar nou net de magie zit. Hoeveel bloemrijker is het om getallen niet te zien als saaie punten op een lijn, maar als stuk voor stuk unieke toverballen met evenzoveel unieke smaken en kleuren!
Dat is wat priemgetallen zijn: de smaken en kleuren van de getallenwereld. Ze zijn nog veel meer. Maar daarover vertel ik de volgende keer. Binnenkort* deel 2 van deze miniserie!









Pak aan!
LikeLike
LikeLike
Prime piece!!
LikeLike
Zenks!
LikeLike
Hoe kon je de prime number shitting bear overslaan??????
http://alpha61.com/primenumbershittingbear/
LikeLike
Heh. Wie weet in deel 2!
LikeLike
Allen voor één!
Zeer onbevredigend, hoe die man met een slinks voorbeeld verdedigt dat 1 geen priemgetal is. Zijn argument is dat 16 te ontbinden is in 4 priemfactoren (2∙2∙2∙2), 8 in 3 (2∙2∙2), 4 in 2 (2∙2), 2 in 1 (2) en dat je bij 1 dan 0 priemfactoren overhoudt. Alsof 2 de enige kandidaat is! Maar je mag bij ontbinden in priemfactoren toch ook andere dan 2 gebruiken? Zo geldt 21 = 3∙7, 55 = 5∙11. Kortom: 1 heeft 0 priemfactoren alleen maar als je eerst 1 als priemgetal hebt uitgesloten – iets wat hij met dit voorbeeld nu juist probeert te beargumenteren.
Zoveel esthetische voordelen heeft het echt niet om 1 uit te sluiten. Iedereen snapt dat vermenigvuldigen met 1 op hetzelfde neerkomt (3∙5 = 1∙1∙1∙3∙5), dus dat evidente voorbehoud (“niet vermenigvuldigen met 1”) doet niets af aan de Hoofdstelling van de Rekenkunde over de uniciteit van de ontbinding in priemfactoren.
Verder voldoet 1 gewoon aan de definitie van priemgetallen: slechts deelbaar door 1 en zichzelf. Het doet er niet toe dat “zichzelf” hier ook 1 is. Je zegt toch ook niet dat 1 geen kwadraat zou zijn omdat 1∙1 toch weer gewoon 1 is? Bij mijn weten zit er bij x = 1 dan ook geen gaatje in de functie f(x) = x².
Ik ben vóór herstel van 1 als priemgetal!
LikeLike
P.S. En zo snapt iedereen ook dat commutativiteit (3∙5 = 5∙3) niets aan die uniciteit afdoet.
LikeLike
Ik vind het wel oogopenend hoe de truimevrouw het opvat:
It looks like there is a blank space on the left. That represents 1, because 1 is the background color, because 1 is a factor of every number.
LikeLike
Precies. En dan nog iets: vanuit de gedachte dat de priemgetallen de ondeelbare atomen van het getallenstelsel zijn, hun bouwstenen, zoals Drabbie schrijft, is het ongerijmd om juist de 1 – de bouwsteen bij uitstek, zou ik zeggen – erbuiten te laten.
LikeLike
Dat is zonder meer waar, maar het boek dat ik momenteel aan het lezen ben (in deel 2 ga ik er reclame voor maken) impliceert dat je 1 beter kunt zien als een subatomair deeltje, omdat hij namelijk niet zozeer een vermenigvuldigings-bouwsteen is als een optel-bouwsteen. Ik heb de passage even niet bij de hand, maar als de tijd het toelaat zal ik haar opzoeken.
LikeLike
Allemaal luchtwindsels! Vermenigvuldigen is namelijk ook gewoon optellen: 3 x 2 = 2 + 2 + 2.
LikeLike
Ja, maar 1 x 1 is niet 1 + 1.
LikeLike
Daarmee bedoelende:
Als je 1 met zichzelf vermenigvuldigt zul je te allen tijde 1 blijven houden. Pas als je hem bij zichzelf gaat optellen kun je er nieuwe getallen mee maken. Ik heb ze even niet allemaal gecheckt want anders worden mijn tapas koud, maar ik ben vrij zeker dat 1 het enige natuurlijke getal is met die eigenschap.
LikeLike
Mm. Daar heb je een punt. Zullen we anders gewoon zeggen: 1 = 1?
LikeLike
Nou, voor deze keer dan.
LikeLike
Priemgetallen zijn cool. De mevrouw met de priemtrui wordt ook cool als je leest hoe ze erover nagedacht heeft :). En priemgetallen zijn dus niet eenzaam (weet niet of je de ‘van’ in de boektitel zo moet opvatten overigens, want ik heb het boek niet gelezen)…
En er ontbreekt een alfa in je ‘atomos’. Veel plezier in Madrid!
LikeLike
’t Is maar hoe je het bekijkt.
Priemgetallen zijn alleen deelbaar door 1 en door zichzelf. Ze staan op hun plaats in de oneindige rij natuurlijke getallen, zoals allemaal tussen twee ingeklemd, maar verder uit elkaar dan de andere. Het zijn argwanende, eenzame getallen en daarom vond Mattia ze prachtig. Soms dacht hij dat ze per ongeluk in die rij waren terechtgekomen, dat ze erin vastzaten als pareltjes in een parelsnoer. Maar op andere momenten vermoedde hij dat ook zij misschien net zo hadden willen zijn als de andere, gewone getallen, maar dat ze daar om de een of andere reden niet toe in staat waren. Die tweede overweging overviel hem vooral ’s avonds, in de chaotische kluwen van beelden vlak voor je in slaap valt, als de geest te zwak is om jezelf iets wijs te maken.
Tijdens college in het eerste jaar had Mattia geleerd dat er onder de priemgetallen nog specialere getallen waren. Die noemden wiskundigen tweelingpriemgetallen: dat zijn paren van priemgetallen die vlak bij elkaar staan, zo goed als naast elkaar zelfs, want ertussenin staat altijd een even getal dat ze belet elkaar echt te raken. Getallen zoals 11 en 13, 17 en 19, 41 en 43. Als je het geduld hebt om door te tellen, kom je erachter dat die paren steeds zeldzamer worden. Je stuit op steeds geïsoleerdere priemgetallen, verdwaald in die stille, ritmische, louter uit getallen bestaande ruimte, en je krijgt het angstige voorgevoel dat de paren die je tot dan toe hebt gevonden op toeval berusten, dat elk getal in wezen voorbestemd is alleen te blijven. En dan, net als je op het punt staat het op te geven, als je geen zin meer hebt om te tellen, stuit je op nog twee tweelingpriemgetallen die zich aan elkaar vastklampen. Wiskundigen zijn het erover eens dat er, hoe lang je ook doorgaat, altijd weer twee zullen zijn, al kan niemand zeggen waar, zolang ze nog niet zijn ontdekt.
Mattia dacht dat Alice en hij zo waren, twee tweelingpriemgetallen, alleen en verloren, vlak bij elkaar, maar niet dicht genoeg om elkaar echt te raken.
(Hfst 21)
LikeLike